Free shipping on all products - $3 Service charge per order

Blending in Harmony with Nature

Imani essential oil synergies and formulas are designed using the Golden Ratios to develop combinations with beauty and effectiveness in harmony with the nature from which they came.

The Golden Mean

By Brian Skinness

This journey into the Golden Mean begins with Leonardo Fibonacci da Pisa. Fibonacci was a mathematician born in Pisa, Italy around 1180 A.D. Although not widely known, the contributions of Fibonacci to the progress of mankind is remarkable. It was his "Book of Calculations," the Liber Abaci, that offered an alternative to the awkward Roman numeral system. In Liber Abaci, Fibonacci further developed the numeric symbol system of 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9, known as the Hindu-Arabic system used today. With the spirit of renaissance, Fibonacci laid the groundwork for widespread advancement in the fields of physics, astronomy and engineering.

Fibonacci Sequence

Fibonacci Sequence Leonardo Fibonacci da Pisa is credited with the discovery and application of a sequence of numbers known today as the Fibonacci Sequence. The Fibonacci Sequence begins with one (1) and adds the previous to get to the next in an infinite progression. 1, 1, 2, 3, 5, 8 ,13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, to infinity~

The Golden Ratio of Phi

The Golden Ratio of Phi The Fibonacci Sequence introduces the Golden Ratio of Phi. Phi is irrational, meaning that it cannot be precisely expressed as the ratio of any two numbers, and there is an endless series of non-repeating digits past the decimal point. Although not precise, an approximation of Phi is produced by dividing any Fibonacci number by the Fibonacci number preceding it. Phi = 1.618033988... 377 / 233 = 1.618025751 6765 / 4181 = 1.618033963 As the Fibonacci numbers approach infinity, the quotient of each successive division alternates above and below true Phi drawing nearer to it in a Golden Ratio.

Something Unique

This is the only ratio where alternating the numerator and denominator yields the same digits past the decimal point.

610 / 377 = 1.618 : 377 / 610 = .618 Converting the ratio of .618 into a percentage yields 61.8%. The compliment of 61.8% is 38.2% since they equal one (1) when added together. Both 61.8% and 38.2% are used to employ the Golden Mean in creative expression.

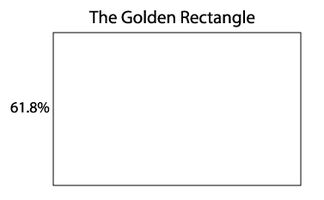
The Golden Rectangle

Dividing a line into segments of 61.8% and 38.2% produces a Golden Section.

A rectangle whose short sides are 61.8% the length of the long sides is a Golden Rectangle. The Golden Rectangle is among the most pleasing shapes.

Squares and Golden Rectangles

By dividing the Golden Rectangle in a Golden Section, a square and smaller Golden Rectangle are formed. The square has 61.8% of the square area of the larger Golden Rectangle and 161.8% of the area of the smaller Golden Rectangle. The smaller Golden rectangle has 38.2% of the area of the larger Golden Rectangle and 61.8% of the area of the square. The smaller Golden Rectangle can be divided repeatedly in a Golden Section.

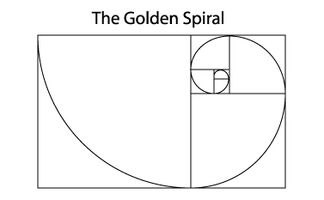
The Golden Spiral

A Golden Spiral is formed by drawing a quarter circle in each square of the segmented Golden Rectangle

The Golden Mean in Nature

Golden Ratios are ubiquitous in nature, showing up in the length of our arm divided at the elbow and wrist in Golden Sections, to the seed distribution of sunflower seeds or barrel cacti, to draining water, the nautilus shell , pine cones, to spiral galaxies. The Golden Mean is indeed a Universal Principle of Organization.